క్వాంటం సంఖ్య

ఉపోద్ఘాతం

బోర్ నమూనాలో ఎలక్ట్రానుల గతులు

అణువు (atom) నిర్మాణ శిల్పం అర్థం చేసుకునే ప్రయత్నంలో రకరకాల నమూనాలు వాడుకలోకి వచ్చేయి. వీటిల్లో ముందుగా ప్రాచుర్యం లోనికి వచ్చినది నీల్స్ బోర్ ప్రతిపాదించిన నమూనా. ఈ బోర్ నమూనాలో అణుగర్భంలో ఒక కేంద్రకము (nucleus), దాని చుట్టూ ఎలక్ట్రానులు నిర్దిష్టమైన దూరాలలో ప్రదక్షణాలు చేస్తూ ఉంటాయి. తక్కువ శక్తి గల ఎలక్ట్రానులు కేంద్రకానికి దగ్గరగా ఉన్న కక్ష్యల (orbits) వెంబడి, ఎక్కువ శక్తి ఉన్న ఎలక్ట్రానులు కేంద్రకానికి దూరంగా ఉన్న కక్ష్యల వెంబడి ప్రదక్షణలు చేస్తూ ఉంటాయి. అందుకని ఈ కక్ష్యల దూరాలని n= 1, 2, 3... అనుకుంటూ పూర్ణాంకాలుగా సూచించడం ఆచారం అయిపోయింది. ఈ n ని మొదటి గుళిక (క్వాంటం) సంఖ్య అంటారు. కనుక n విలువ తెలిస్తే ఎలక్ట్రాను ఎంత శక్తివంతమైన స్థితిలో ఉందో తెలుస్తుంది. ఇది కక్ష్య సైజుని (పరిమాణంని), లేదా శక్తి స్థాయిని సూచిస్తుంది. ఈ n విలువ పెరిగే కొద్ది కక్ష్య సైజు, శక్తి పెరుగుతాయి. ఈ n విలువ 1 నుండి బాహ్య ఎలక్ట్రాన్ కలిగి వున్న స్థాయి వరకు ఉంటుంది.

ఉదాహరణకు సీజీయం (Cs) లో బాహ్య ఎలక్ట్రాన్ శక్తి స్థాయి n = 6 గల కోశం లో ఉండడం వల్ల సిజియంలో ఎలక్ట్రాన్ యొక్క n విలువ 1 నుండి 6 దాకా ఉండవచ్చు.

అణువు స్థితి

ఎలక్ట్రాను పరిస్థితి (state) ని వర్ణించడానికి అది ఎంత శక్తివంతంగా ఉందో చెప్పినంత మాత్రాన సరిపోదు. (ఒక మనిషిని వర్ణించాలంటే ఆ మనిషి పొడుగు, బరువు, జుత్తు రంగు, కళ్ళ రంగు, వగైరాలు ఎలా కావాలో అదే విధంగా ఒక ఎలక్ట్రాను స్థితిని వర్ణించడానికి అది కేంద్రానికి ఎంత దూరంలో ఉందో (అనగా, n విలువ) చెప్పాలి, ఎంత జోరుగా ప్రదక్షిణం చేస్తున్నాదో (అనగా, కోణీయ వేగం, l విలువ) చెప్పాలి. దీనినే ఇంగ్లీషులో అజిముతల్ క్వాంటం నంబర్ అంటారు. దీనిని ల్ తో సూచిస్తారు. ఇది రెండవ క్వాంటమ్ సంఖ్య. ఇది కక్ష్య కోణీయ వేగం (orbital angular velocity) యొక్క పరిమాణం ఇస్తుంది. దీనిని కోణీయ క్వాంటం సంఖ్య అని కూడా అంటారు. (రసాయన శాస్త్రంలోనూ, స్పెక్ట్రో స్కొపీ లోనూ l = 0 అయితే n ఆర్బిటల్ అంటారు. అలాగే l = 1 అయితే p, ఇంకా l = 3 అయితే f ఆర్బిటల్ అనీ అంటారు.

అదే విధంగా ఎలక్ట్రాను యొక్క అయస్కాంత కదలిక, (m విలువని మేగ్నెటిక్ క్వాంటం నంబర్ అంటారు. ఆ చేసే ప్రదక్షిణంలో భ్రమణం (spin) ఉందో లేదో సూచించే (s విలువని స్పిన్ క్వాంటం నంబర్ అంటారు. వీటన్నిటిని (అనగా, n, l, m, s,) కలిపి గుళిక సంఖ్యలు (quantum numbers) అంటారు.

అధునాతన గుళిక వాదంలో విగతులు

మేఘాలులా ఉన్న విగతుల స్వరూపాలు

గుళిక వాదంలో గతి (orbit), విగతి (orbital), శక్తి స్థానం (energy level), కోశం (shell) అనే మాటలు తరచుగా వినిపిస్తూ ఉంటాయి . స్థూలంగా ఈ మాటలు అన్నీ దరిదాపుగా ఒకే భావాన్ని చెబుతాయి. సూక్ష్మంగా ఈకలు పీకితే చిన్న చిన్న తేడాలు కనబడతాయి. ఒకే భావానికి ఇన్ని మాటలు ఉండడానికి కారణం ఏమిటంటే మొదట్లో ఈ భావాలు సమగ్రంగా మన అవగాహనలోకి రాలేదు. ఇప్పుడు అవగాహన పెరిగింది కానీ బంకనక్కిరికాయల్లా ఈ పాత మాటలు మనని పట్టుకు వేలాడుతున్నాయి. ఇప్పుడు పొమ్మంటే పోవు. పుస్తకాలు అన్నీ తిరగ రాయడం సాధ్యమా?

గుళిక వాదంలో తారసపడే సాంకేతిక పదం “గతి” ఇంగ్లీషులో “ఆర్బిట్” (orbit) తో సమానం. సౌరకుటుంబంలో గ్రహ గతులని “ఆర్బిట్” లు అంటారు. (వీటిని తెలుగులో కక్ష్యలు అని కూడా అంటారు.) ఇవి ఒకే తలంలో ఉండే గ్రహ సంచార రేఖలు. ఇదే విధంగా ఎలక్ట్రానులు కూడా ఒక కేంద్రకం చుట్టూ ఒక నియమితమైన తలంలో, ఒక నియమితమైన మార్గంలో ప్రయాణం చేస్తున్నాయని మనం ఊహించుకుంటే అప్పుడు ఎలక్ట్రాను ప్రయాణించే మార్గాన్ని కూడా “గతి” అనో, “కక్ష్య” అనో పిలవచ్చు. (An orbit is a planar or two-dimensional circular pathway. An orbit follows Newton’s laws of motion.) అనగా, గతి అనే దానిని ఊహించుకోవాలంటే ఒక తీగకి పూసని గుచ్చి, ఆ తీగని గుండ్రంగా అమర్చినప్పుడు తీగ “గతి” అవుతుంది, పూస ఎలక్ట్రాను అవుతుంది.

కానీ ఆధునిక గుళిక వాదం, ప్రత్యేకించి హైజన్బర్గ్ అనిర్దిష్ట సూత్రం (Uncertainity Principle), ప్రకారం ఎలక్ట్రాను ఫలానా మార్గం వెంబడి ప్రయాణిస్తున్నదని నిర్ధారించి చెప్పలేము. కనుక గుళిక వాదంలో “ఆర్బిట్” (గతి, కక్ష్య) అన్న మాటకి అర్థం లేదు. గుళిక వాదంలో ఎలక్ట్రాను ఆక్రమించిన ప్రదేశం విస్తృతం, త్రి-మితీయం (3-dimensional) కనుక ఇలా “వికసించిన” ప్రదేశాన్ని సూచించడానికి ఇంగ్లీషులో “ఆర్బిటల్” అని కొత్త పేరు సృష్టించేరు. “విస్తరించిన గతి” లేదా “వికసించిన గతి” కనుక దీనిని మనం తెలుగులో “విగతి” అనొచ్చు. దీనిని తెలుగులో కర్పరం అని కూడా అంటారట!

ఒక త్రి-మితీయ ప్రదేశంలో ఎలక్ట్రాను ఆక్రమించిన ప్రదేశాన్ని విగతి అన్నాం కదా. ఇది త్రి-మితీయ ప్రదేశంలో ఉంది కనుక ఒక ఎలక్ట్రాను ఆక్రమించిన ప్రదేశానికి పొడుగు, వెడల్పు, లోతు ఉంటాయి. అనగా ఎలక్ట్రాను ఆక్రమించిన ప్రదేశం మేఘం రూపంలో ఉంటుందని ఊహించుకోవచ్చు. ఈ మేఘం కూడా - దాంట్లో నిక్షిప్తమైన శక్తిని బట్టి - రకరకాల బుడగలు రూపంలో ఉంటుందని కూడా మనం ఊహించుకోవచ్చు. ఈ బుడగ రూపాలనే ఇంగ్లీషులో “ఆర్బిటల్స్” అంటారు, తెలుగులో “విగతులు” అంటున్నాం. అనగా, విగతి అనేదానిని ఊహించుకోవాలంటే రబ్బరు బుడగ ఆకారం ఒక విగతి అవుతుంది, రెండు బుడగలని ఊది, వాటి మూతుల దగ్గర ముడి వేస్తే వచ్చే ఆకారం మరొక విగతి అవుతుంది. మూడు బుడగలని ఊది, వాటి మూతుల దగ్గర ముడి వేస్తే వచ్చే ఆకారం మరొక విగతి అవుతుంది.

సారణి 1: గతి, విగతి అనే భావాల మధ్య పోలికలు, తేడాలు

గతి (orbit)

విగతి (orbital)

1. కేంద్రకం చుట్టూ ఒక నిర్దిష్టమైన గుండ్రటి పరిధి. ఈ పరిధి వెంబడి గానుగెద్దులా ఎలక్ట్రాను ప్రయాణిస్తున్నదని అనుకుంటాం. 2. ఎలక్ట్రాను ప్రయాణించే పరిధి ఒక చదునైన ప్రదేశంలో ఉన్నట్లు ఉహించుకుంటాం. 3. ఒకొక్క గతిలో ఎలక్ట్రానులు పడతాయి. ఇక్కడ అనేవి గతిని నిర్దేశించే సంఖ్యలు. 4. గతులు దిశా శీలాన్ని ప్రదర్శించలేవు కనుక బణువుల ఆకారాలకి కారణాలు చెప్పలేవు. 5. నిర్దిష్టమైన గతులు అనే భావం హైజెన్బర్గ్ అనిశ్చిత సూత్రానికి విరుద్ధం.

1. కేంద్రకం చుట్టూ అనిర్దిష్టంగా ఆవరించి ఉన్న మేఘం లాంటి ప్రదేశం. ఈ త్రి-మితీయ ప్రదేశంలో ఎలక్ట్రాను ఎక్కడైనా ఉండవచ్చు. 2. ఎలక్ట్రాను ఆవరించే ప్రదేశం ఒక త్రి-మితీయ ఆవరణలో ఉన్నట్లు ఉహించుకుంటాం. 3. ఒకొక్క విగతిలో రెండు కంటే ఎక్కువ ఎలక్ట్రానులు పట్టవు. 4. విగతులు దిశా శీలాన్ని ప్రదర్శించగలవు కనుక బణువుల ఆకారాలకి కారణాలు చెప్పగలవు. 5. విగతులు అనే భావం హైజెన్బర్గ్ అనిశ్చిత సూత్రానికి విరుద్ధం కాదు.

కోశం (shell), శక్తి స్థానం (energy level), విగతి (orbital)

ఇప్పుడు కోశం (shell), శక్తి స్థానం (energy level), విగతి (orbital) అనే భావాలకి నిర్దిష్టమైన నిర్వచనాలు ఇద్దాం.

• ప్రాథమిక గుళిక సంఖ్య n సమానమైన ఎలక్ట్రానులన్నీ ఒకే కోశానికి చెందుతాయి.
• ఒక కోశంలో (అనగా, ఒకే n విలువ ఉన్న సందర్భాలలో) దిగంశ గుళిక సంఖ్యలు (అజిముతల్ క్వాంటం సంఖ్యలు) (అనగా, l విలువలు) సమానమైన సందర్భాలలో ఎలక్ట్రానులన్నీ ఒకే ఉప-కోశానికి చెందుతాయి.
• ఒక ఉప-కోశంలో (అనగా, ఒకే n విలువ, ఒకే l విలువ, ఒకే m విలువ) ఉన్న ఎలక్ట్రానులన్ని ఒకే విగతికి చెందుతాయి. అనగా, ఒకే విగతిలో ఉన్న ఎలక్ట్రానులన్ని ఒకే శక్తితో, ఒకే ఆకారంలో, ఒకే దిశాశీలంతో ఉంటాయి.
• బోర్ నమూనాలో కనిపించే గతులు (orbits), ఇక్కడి కోశాలు (shells) - రెండూ ఒకే భావాన్ని చెబుతాయి. ఈ కోశాలని లెక్కపెట్టడానికి n = 1, 2, 3,... అనే గుళిక సంఖ్యలని వాడతారు.
• ఉపకోశం: కోశాలలో ఒకటో, రెండో, మూడో,... , ఉప-కోశాలు ఉంటాయి. వీటికి s, p, d, f అనే పేర్లు పెట్టేరు. ఉదాహరణకి మొదటి (n = 1) కోశంలో ఒకే ఒక ఉప-కోశం n ఉంటుంది. రెండవ (n = 2) కోశంలో రెండు ఉప-కోశాలు s, p ఉంటాయి. మూడవ (n = 3) కోశంలో మూడు ఉప-కోశాలు s, p, d ఉంటాయి. అటుపైన అన్ని కోశాలలో నాలుగేసి ఉప-కోశాలు s, p, d, f లు ఉంటాయి.
• విగతి (orbital): విగతి అంటే కేంద్రకం చుట్టూ ఉన్న ప్రదేశంలో ఎలక్ట్రాను కనబడే సంభావ్యతని తెలియజేసేది. ప్రతి ఉప-కోశంలోను ఒకటో, అంతకంటే ఎక్కువో విగతులు పడతాయి. నిర్దిష్టంగా చెప్పాలంటే -

• • ఉప-కోశం s లో 1 విగతి పడుతుంది లేదా 2 ఎలక్ట్రానులు పడతాయి.
  • ఉప-కోశం p లో 3 విగతులు పడతాయి లేదా 6 ఎలక్ట్రానులు పడతాయి.
  • ఉప-కోశం d లో 5 విగతులు పడతాయి లేదా 10 ఎలక్ట్రానులు పడతాయి.
  • ఉప-కోశం f లో 7 విగతులు పడతాయి లేదా 14 ఎలక్ట్రానులు పడతాయి.

ఈ సమాచారాన్నంతటిని ఈ దిగువ చూపిన సారణిలో సంక్షిప్తపరచవచ్చు.

ష్రోడింగర్ నమూనా ప్రకారం కోశం (shell), ఉప-కోశం, విగతి (orbital) అంటే ఏమిటో వివరించే బొమ్మ.

సారణి 2: కోశం (shell), ఉప-కోశం, విగతి (orbital) అమరిక

	ℓ = 0	ℓ = 1	ℓ = 2	ℓ = 3	ℓ = 4	...
n = 1	$m_{\ell }=0$
n = 2	0	−1, 0, 1
n = 3	0	−1, 0, 1	−2, −1, 0, 1, 2
n = 4	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3
n = 5	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3	−4, −3, −2, −1, 0, 1, 2, 3, 4
...	...	...	...	...	...	...

సారణి 3. కోశం (shell), ఉప-కోశం, విగతి (orbital)

	s (ℓ = 0)	p (ℓ = 1)			d (ℓ = 2)					f (ℓ = 3)
	m = 0	m = 0	m = ±1		m = 0	m = ±1		m = ±2		m = 0	m = ±1		m = ±2		m = ±3
	s	pz	px	py	dz2	dxz	dyz	dxy	dx2−y2	fz3	fxz2	fyz2	fxyz	fz(x2−y2)	fx(x2−3y2)	fy(3x2−y2)
n = 1
n = 2
n = 3
n = 4
n = 5										. . .	. . .	. . .	. . .	. . .	. . .	. . .
n = 6					. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
n = 7		. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .

ఒక ఉపమానం

విగతులని ఉహించుకుందుకి ఒక “తిరకాసు భవనం” ఉపమానం చెబుతాను. ఈ తిరకాసు భవనం మొదటి అంతస్థులో ఒకే ఒక గది ఉంటుంది. ఈ గది మీద 1s అని రాసి ఉంటుంది. ఆ గదిలో ఒక మంచం. ఆ మంచం మీద రెండు ఎలక్ట్రానులు పడతాయి - ఒకటి ఊర్ధ్వ ముఖం తోటి 1s¹, ఒకటి అధో ముఖం తోటి 1s² ఈ గది అట్టడుగున ఉంటుంది కనుక ఇది చాల తక్కువ శక్తి స్థానంలో ఉంటుంది.

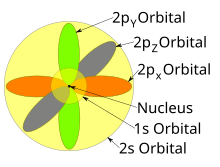
“తిరకాసు భవనం” రెండవ అంతస్థులో రెండు వసారాలు ఉంటాయి. మొదటి వసారాలో ఒక గది, ఆ గది మీద 2s అని రాసి ఉంటుంది. రెండవ వసారాలో మూడు గదులు ఉంటాయి, వాటి మీద 2p_x, 2p_y, 2p_z అని రాసి ఉంటాయి. ఒకొక్క గదిలో ఒకొక్క మంచం, ఒకొక్క మంచం మీద రెండేసి ఎలక్ట్రానులు - ఒకటి ఊర్ధ్వ ముఖం తోటి, ఒకటి అధో ముఖం తోటి ఉంటాయి. ఈ రెండవ అంతస్తు మొదటి అంతస్తు కంటే ఎక్కువ శక్తి స్థానంలో ఉంటుంది.

“తిరకాసు భవనం” మూడవ అంతస్థులో మూడు వసారాలు ఉంటాయి. మొదటి వసారాలో ఒక గది, ఆ గది మీద 3s అని రాసి ఉంటుంది. రెండవ వసారాలో మూడు గదులు ఉంటాయి, వాటి మీద 3p_x, 3p_y, 3p_z అని రాసి ఉంటాయి. మూడవ వసారాలో 5 గదులు ఉంటాయి, వాటి మీద 3d₁, 3d₂, 3d₃, 3d₄, 3d₅ అని రాసి ఉంటాయి. ఒకొక్క గదిలో ఒకొక్క మంచం, ఒకొక్క మంచం మీద రెండేసి ఎలక్ట్రానులు - ఒకటి ఊర్ధ్వ ముఖం తోటి, ఒకటి అధో ముఖం తోటి ఉంటాయి. ఈ మూడవ అంతస్తు రెండవ అంతస్తు కంటే ఎక్కువ శక్తి స్థానంలో ఉంటుంది. ఎలక్ట్రానులని గదులలో నింపినప్పుడు అడుగునుండి పైకి ఒక పద్ధతిలో నింపుకుంటూ పోవాలి.